元素的笔记

题目描述

大家都知道，斐波那契数列是满足如下性质的一个数列：

$$F_n = \left\{\begin{aligned} 1 \space (n \le 2) \\ F_{n-1}+F_{n-2} \space (n\ge 3) \end{aligned}\right.$$

请你求出 F_n mod  10⁹ + 7 的值。

猫和老鼠所在的庄园可以视为一张由 n 个点和 m 条带权无向边构成的连通图。结点依次以 1, 2, …, n 编号，结点 i（1 ≤ i ≤ n）有价值为 c_i 的奶酪。在 m 条带权无向边中，第 i（1 ≤ i ≤ m）条无向边连接结点 u_i 与结点 v_i，边权 w_i 表示猫和老鼠通过这条边所需的时间。

猫窝位于结点 a，老鼠洞位于结点 b。对于老鼠而言，结点 u 是安全的当且仅当：

• 老鼠能规划一条从结点 u 出发逃往老鼠洞的路径，使得对于路径上任意结点 x（包括结点 u 与老鼠洞）都有：猫从猫窝出发到结点 x 的最短时间严格大于老鼠从结点 u 沿这条路径前往结点 x 所需的时间。

老鼠在拿取安全结点的奶酪时不存在被猫抓住的可能，但在拿取不是安全结点的奶酪时则不一定。为了确保万无一失，老鼠决定只拿取安全结点放置的奶酪。请你计算老鼠所能拿到的奶酪价值之和。

题目描述

小杨所在班级共有 n 位同学，依次以 1, 2, …, n 标号。这 n 位同学想排成一行队伍，其中有些同学之间关系非常好，在队伍里需要排在相邻的位置。具体来说，有 m 对这样的关系（m 是一个非负整数）。当 m ≥ 1 时，第 i 对关系（1 ≤ i ≤ m）给出 a_i, b_i，表示排队时编号为 a_i 的同学需要排在编号为 b_i 的同学前面，并且两人在队伍中相邻。

现在小杨想知道总共有多少种排队方式。由于答案可能很大，你只需要求出答案对 10⁹ + 7 取模的结果。

闲着没事写的

一天有 T(1 ≤ T ≤ 10⁶) 个时段。约翰正打算安排他的 N(1 ≤ N ≤ 2.5 × 10⁴) 只奶牛来值班，打扫打扫牛棚卫生。每只奶牛都有自己的空闲时间段 $ S_i,E_i$，只能把空闲的奶牛安排出来值班。而且，每个时间段必需有奶牛在值班。

那么，最少需要动用多少奶牛参与值班呢？如果没有办法安排出合理的方案，就输出 −1。

如题，已知一个数列 {a_i}，你需要进行下面两种操作：

1. 将某区间每一个数加上 k。
2. 求出某区间每一个数的和。

农夫约翰有 N 头奶牛正在过乱头发节。

每一头牛都站在同一排面朝右，它们被从左到右依次编号为 1, 2, ⋯, N。编号为 i 的牛身高为 h_i。第 N 头牛在最前面，而第 1 头牛在最后面。

对于第 i 头牛前面的第 j 头牛，如果 h_i > h_i + 1, h_i > h_i + 2, ⋯, h_i > h_j，那么认为第 i 头牛可以看到第 i + 1 到第 j 头牛。

定义 C_i 为第 i 头牛所能看到的牛的数量。请帮助农夫约翰求出 C₁ + C₂ + ⋯ + C_N。

给出一个长度为 n 的序列 a_i，求出下列式子的值：

$$\sum_{i=1}^{n} \sum_{j=i}^{n} (\max_{i\le k\le j} a_k-\min_{i\le k\le j} a_k)$$

即定义一个子序列的权值为序列内最大值与最小值的差。求出所有连续子序列的权值和。

设 T = (V, E, W) 是一个无圈且连通的无向图（也称为无根树），每条边都有正整数的权，我们称 T 为树网（treenetwork），其中 V，E 分别表示结点与边的集合，W 表示各边长度的集合，并设 T 有 n 个结点。

路径：树网中任何两结点 a，b 都存在唯一的一条简单路径，用 d(a, b) 表示以 a, b 为端点的路径的长度，它是该路径上各边长度之和。我们称 d(a, b) 为 a, b 两结点间的距离。

D(v, P) = min {d(v, u)}, u 为路径 P 上的结点。

树网的直径：树网中最长的路径称为树网的直径。对于给定的树网 T，直径不一定是唯一的，但可以证明：各直径的中点（不一定恰好是某个结点，可能在某条边的内部）是唯一的，我们称该点为树网的中心。

偏心距 ECC(F)：树网 T 中距路径 F 最远的结点到路径 F 的距离，即

ECC(F) = max {D(v, F), v ∈ V}

任务：对于给定的树网 T = (V, E, W) 和非负整数 s，求一个路径 F，他是某直径上的一段路径（该路径两端均为树网中的结点），其长度不超过 s（可以等于 s），使偏心距 ECC(F) 最小。我们称这个路径为树网 T = (V, E, W) 的核（Core）。必要时，F 可以退化为某个结点。一般来说，在上述定义下，核不一定只有一个，但最小偏心距是唯一的。

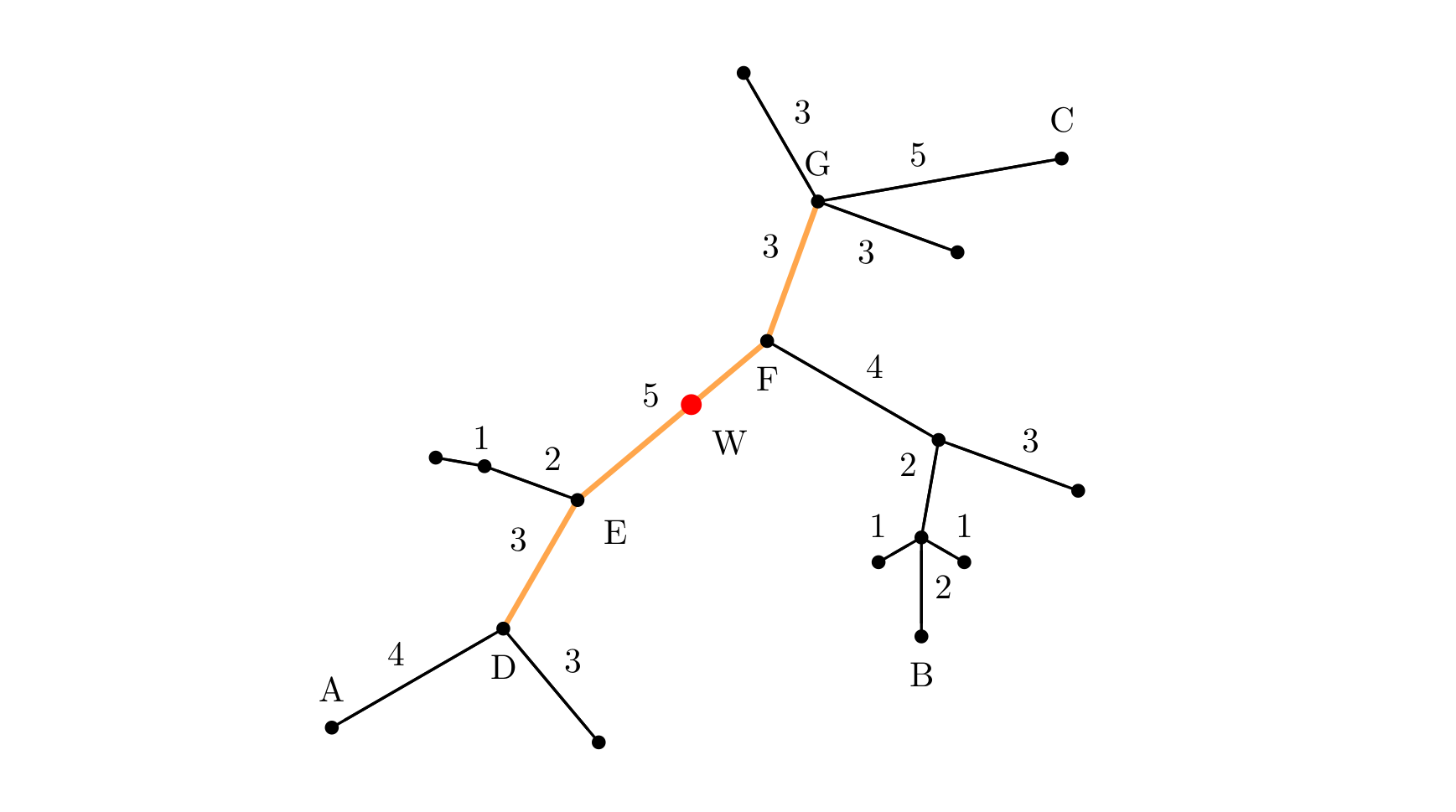
下面的图给出了树网的一个实例。图中，A − B 与 A − C 是两条直径，长度均为 20。点 W 是树网的中心，EF 边的长度为 5。如果指定 s = 11，则树网的核为路径DEFG（也可以取为路径DEF），偏心距为 8。如果指定 s = 0（或 s = 1、s = 2），则树网的核为结点 F，偏心距为 12。

21 世纪，许多人得了一种奇怪的病：起床困难综合症，其临床表现为：起床难，起床后精神不佳。作为一名青春阳光好少年，atm 一直坚持与起床困难综合症作斗争。通过研究相关文献，他找到了该病的发病原因：在深邃的太平洋海底中，出现了一条名为 drd 的巨龙，它掌握着睡眠之精髓，能随意延长大家的睡眠时间。正是由于 drd 的活动，起床困难综合症愈演愈烈，以惊人的速度在世界上传播。为了彻底消灭这种病，atm 决定前往海底，消灭这条恶龙。历经千辛万苦，atm 终于来到了 drd 所在的地方，准备与其展开艰苦卓绝的战斗。drd 有着十分特殊的技能，他的防御战线能够使用一定的运算来改变他受到的伤害。具体说来，drd 的防御战线由 n 扇防御门组成。每扇防御门包括一个运算 op 和一个参数 t，其中运算一定是 OR, XOR, AND 中的一种，参数则一定为非负整数。如果还未通过防御门时攻击力为 x，则其通过这扇防御门后攻击力将变为 x op t。最终 drd 受到的伤害为对方初始攻击力 x 依次经过所有 n 扇防御门后转变得到的攻击力。

由于 atm 水平有限，他的初始攻击力只能为 0 到 m 之间的一个整数（即他的初始攻击力只能在 0, 1, …, m 中任选，但在通过防御门之后的攻击力不受 m 的限制）。为了节省体力，他希望通过选择合适的初始攻击力使得他的攻击能让 drd 受到最大的伤害，请你帮他计算一下，他的一次攻击最多能使 drd 受到多少伤害。